1 Introduction

Creative music systems are often criticised as not “really” being creative per se; underlying this criticism is the belief that the actual human programmer is the true source of creativity. However, machine learning has made such criticisms more difficult to maintain, as a machine may acquire knowledge from data, constructing a new conceptual space without human intervention, creating new unforeseen output (Wiggins et al., 2009). Adaptability, flexibility, independence, and autonomy are features associated with creativity (see key components of creativity in Jordanous (2013)); general representations and machine learning techniques allow creative systems to be open to new environments, to evolve, to transform existing concepts, and to construct new ones, creating new and unexpected results.

A model of creativity has been proposed by Boden (2009) whereby a conceptual space may be explored by an agent in order to: generate new creative instances (exploratory creativity); transform the rules of the conceptual space, changing the conceptual space itself (transformational creativiy); or, create new blended spaces by combining different conceptual spaces that share structural similarities (combinational creativity). In the current study the conceptual spaces are learned in a bottom-up fashion from data, and are structured in a modular way so as to allow (at a later stage) to combine different modules from different spaces, thus creating new blended spaces. At this stage, the system is indicated to exhibit exploratory creativity, by composing harmonies that potentially excess the harmonic borders of a corpus.

This article focuses on melodic harmonisation as a creative musical act. Some researchers follow the knowledge-engineering approach whereby experts encode the essential rules for harmonisation in a certain tonal style (from the Bach chorale expert system by Ebcioglu (1988) to the explicitly structured knowledge paradigm by Phon-Amnuaisuk & Wiggins (1999) and Phon-Amnuaisuk et al. (2006)). In recent years, more attention has been given to probabilistic approaches that learn harmony from musical data, using techniques such as Hidden Markov Models, N-grams, probabilistic grammars, and inductive logic programming (Steedman, 1996; Rohrmeier, 2011; Conklin, 2002; Scholz et al., 2009; Pérez-Sancho et al., 2009; Raphael & Stoddard, 2004; Whorley et al., 2013; Dixon et al., 2010; Granroth-Wilding & Steedman, 2014). Such models automatically derive harmonic structure from training data and are thus more flexible than rule-based systems; however, they are usually applied to very narrow well-circumscribed tonal styles (e.g., Bach chorales, hymns or blues harmonies) and they generate acceptable harmonic progressions only within the corresponding learned harmony (i.e., they cannot create new harmonies beyond the learned space).

This article describes a creative melodic harmonisation system that can assist a user in generating new conventional or unconventional sequences of chords for a given melody. The creative melodic harmonisation assistant is based on a novel General Chord Type representation (Cambouropoulos et al., 2014) that allows the system to extract appropriate chord types from diverse harmonic idioms. For any harmonic idiom, the system learns from a set of pieces (harmonic reductions) the chord types that are relevant for the specific style, extracts probabilistic information on the most likely chord transitions (first order transition tables), examines phrase endings with a view to establishing common endings/cadences, and learns basic features of voice-leading (bass movement in relation to melodic motion, chord inversions and omission/duplication of chord notes). This information constitutes a conceptual space that characterises a specific harmonic idiom and is used to create original harmonisations for previously unheard melodies.

Apart from learning harmony from a particular harmonic style and producing new harmonisations in this style, the present article explores other creative aspects of the proposed melodic harmonisation assistant that diverge from a learned harmonic style (not automated in this phase). Firstly, a user may assign particular chords to specific melodic notes of a given melody, thus “forcing” the system to explore harmonic regions of the learned harmonic space that are less common (or even alien), giving rise to potentially unexpected harmonisations, expressed as chord sequence paths that accommodate the selected chords. Secondly, a user may choose to harmonise a melody with potentially incompatible learned harmonic styles (e.g., a traditional folk melody with tonal harmony or octatonic harmony, etc.); potential inconsistencies are dealt with manually at this stage (automation of such processes is under development). The ultimate goal of this research is to enable a system to create original harmonisations by combining harmonic components of different harmonic spaces; such creative blending aspects are explored in Zacharakis et al. (2015) and Cambouropoulos et al. (2015), and is part of ongoing research.

The proposed melodic harmonisation assistant is original in the following ways:

1. Harmony is learned in an idiom-independent manner i.e., harmonic features are acquired via machine learning for various tonal and non-tonal systems.
2. The system allows the exploration of a learned harmonic space by user-defined intermediate chords that may lead the system outside its expected course.
3. The creative system can use existing harmonic styles to harmonise melodies with “incompatible” harmonic outlook.

In the following sections the proposed modular probabilistic melodic harmonisation system is presented; this system is able to learn different harmonic aspects (chord types, chord progressions, cadences, and voice-leading) from practically any musical idiom, and can use the acquired harmonic knowledge to harmonise novel melodies in innovative ways. The next section provides a short discussion on previous approaches to melodic harmonisation and an overview of the proposed system. Section 4 analyses the module for constructing chord sequences by automatically employing cadences and allowing user-defined chord constraints. The module for fixing the layout of voices is presented in Section 5 and, finally, several examples of melodic harmonisations in diverse harmonic idioms are presented in Section 6.

2 Melodic Harmonisation: Related Work and Overview of the Proposed System

Among the first approaches to capturing the characteristics of harmony in automated melodic harmonisation were ones that incorporated human expert knowledge, encoded in the form of rules, leading to systems that could harmonise melodies according to explicit stylistic directives (Ebcioglu, 1988). For a review of rule–based systems the reader is referred to Pachet & Roy (2001). A similar approach to rule-based methodologies is the one followed by systems that utilise genetic algorithms (GA), like the ones briefly reviewed in the recent paper by Donnelly & Sheppard (2011) and, also, in Phon-Amnuaisuk & Wiggins (1999). The similarity between these two approaches is that both rely on a set of harmonic rules intended for a specific musical idiom; in the case of the GAs, the employed fitness function quantifies such rules. The advantage of rule–based systems is that they can capture the hierarchical structure of complex musical idioms by, for example, using grammar-related structures for tonal (Rohrmeier, 2011; Koops et al., 2013) or jazz music (Granroth-Wilding & Steedman, 2014).

However, the melodic harmonisation methodologies that utilise rule-based techniques have a major drawback when dealing with melodic harmonisation in many diverse idioms: encoding rules that describe even a simple musical idiom is not always a realisable task, since idioms are abound in complex and often contradicting interrelations between harmonic elements. In order to overcome such shortcomings, the formulation of probabilistic techniques and statistical learning has been proposed. Probabilistic techniques on the one hand can be trained on any musical idiom, given a set of harmonically annotated pieces, while on the other hand they encompass the possibility to take “unusual” decisions if necessary, e.g., if the melody’s implied harmony diverges from the learned harmony. Among many proposed methodologies, Bayesian networks (Suzuki, 2013) and prediction by partial matching (Whorely et al., 2013) have been utilised to construct the bass, tenor and alto voices below a given soprano voice, Hidden Markov Models (HMMs) for constructing chord sequences for a given melody (Raczýnski et al., 2013) and probabalistic graphical models for relative tasks (Paiement et al., 2006).

The main drawback of probabilistic methodologies, especially HMMs, is that they do not capture larger scale dependencies between remote harmonic parts (Pachet et al., 2011). For instance, phrase endings, indicated by cadences, are very distinctive parts of higher-level harmonic structure that are not captured by methodologies that concern chord-to-chord harmonic progressions. Cadences have been studied under different contexts in the computational harmonisation literature. For instance, in Borrel-Jensen & Danielsen (2010) a methodology based on cadences was utilised to evaluate the outcomes of an automatic melodic harmonisation system. The methodologies presented in Allan & Williams (2004) and Hanlon & Ledlie (2002) utilise a backwards propagation of the Hidden Markov model (HMM) methodology, starting from the end and constructing the chord progression in a backwards fashion, highlighting the role of the cadence in reflecting structure. In Yi & Goldsmith (2007) a probabilistic system was presented that rewarded the chord sequences that ended with the perfect cadence, while in Yogev & Lerch (2008) a probabilistic methodology that identifies the probable positions of cadences was introduced. Special consideration of cadences has also been employed in HMM-based methodologies, either with assigning an additional layer of probabilities for the final chords of sequences (Simon et al., 2008) or by fixing ending or intermediate chords in probabilistically produced chord sequences (Kaliakatsos-Papakostas & Cambouropoulos, 2014).

The architecture of the proposed system offers the advantage of preserving structural relations between remote harmonic parts, while at the same time diverse harmonies can be learned from data. Therefore, the merits of rule-based systems are preserved by learning and automatically employing intermediate and final cadences, leading to harmonisations that are structurally consistent. Additionally, the probabilistic nature of the incorporated algorithms allows for radically diverse harmonic idioms to be learned, while the generated harmonisations reflect their characteristics in terms of chord transitions and voicing layout. An additional advantage of the presented system is the fact that the out-put is a harmonic realisation with actual chord notes (not only chord symbols).

The presented harmonic learning system is trained independently on several harmonic aspects that are divided into two groups: chord generation and voicing layout. Fig. 1 illustrates this setting, where “GCT generation” on the left block refers to the generation of chord symbols in the General Chord Type (GCT) representation (Cambouropoulos et al., 2014; Cambouropoulos, 2015), while the right block refers to the materialisation of GCT chords to music by assigning proper voicing layouts, converting the final output to actual MIDI notes. The oval blocks refer to modules that have been trained from data. The arrow leading from the “GCT generation” to the “GCT to MIDI pitches” block indicates the current generative process workflow of the melodic harmoniser: first, chord sequences in GCT form are produced and, afterwards, voicing layout is applied to the composed GCT sequences, providing the finalised output in MIDI format. In turn, the bass voice motion is first defined for the given GCT sequence and the given melody and, afterwards, the intermediate chord notes between bass and melody are fixed.

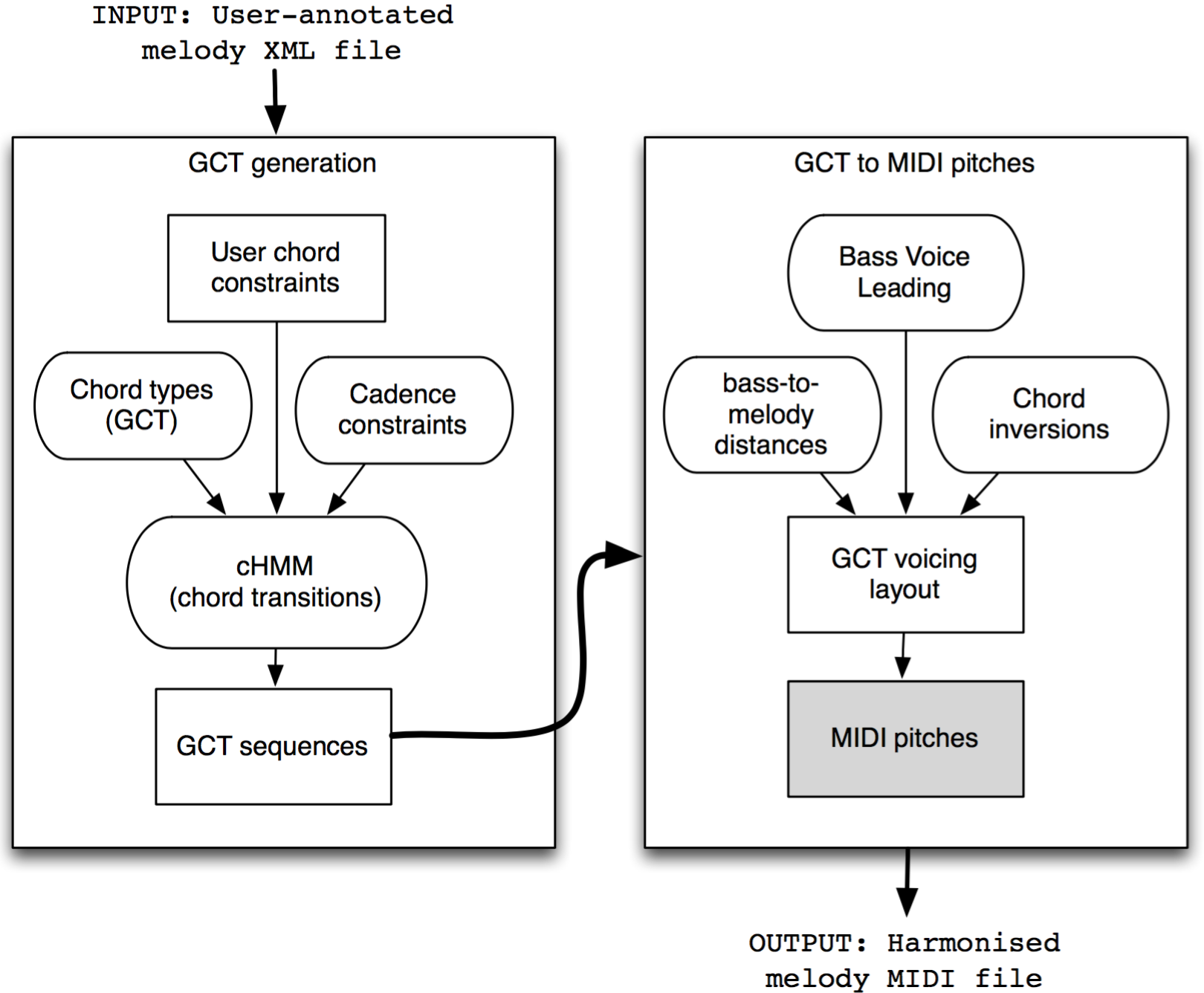
Both the “GCT generation” and the “GCT to MIDI pitches” blocks include modules that learn from data, giving the system the ability to express the characteristics of each learned idiom on several harmonic aspects. The GCT generation block incorporates three learning modules: (a) the “Chord types” module which learns chord types by converting the pitches of the training harmonies to GCTs and organising them into chord type categories, (b) the “Cadence constraints” module that learns and assigns cadences to user-defined positions of phrase endings (preserving high-level structure), and (c) the constraint Hidden Markov Model (cHMM) (Kaliakatsos-Papakostas & Cambouropoulos, 2014) that learns first order GCT chord transitions and performs probabilistic harmonisations given the aforementioned cadence constraints as well as user-defined chord constraints. The “GCT to MIDI pitches” block includes the following learning modules: (a) the “Bass Voice Leading” module that defines the motion of the bass in relation to the melody, (b) the “bass-to-melody distances” that learns statistics about the distances between the bass and the melody for each idiom, and (c) the “Chord inversions” module that learns statistics about the inversions of the learned GCT chords. The aforementioned voice-related modules are contributing to the definition of the bass voice and afterwards, a simple algorithmic process, namely the “GCT voicing layout” module, defines the chord notes between the bass and the melody.

3 Chord Representation and Data Input for Training and Generating

The system learns a given harmonic content given through annotated training data, while it produces new harmonisations according to guidelines provided in the melody input file. Since the processes of training and composing both incorporate many diverse musical idioms, the system learns the available chord types therein (according to their root notes) based on the General Chord Type (GCT) representation (Cambouropoulos et al., 2014). The training data includes the notes on a level of harmonic reduction (manually annotated reductions), where only the most important harmonic notes are included, while additional layers of information are given regarding the tonality and the metric structure of each piece. Accordingly, the format of the user-melody input file includes indications about several desired attributes that the resulting harmonisation should have. The chord representation scheme, the format of the training data, and the user-melodic input file are analysed in the following subsections.

3.1 Representation of Harmony in Diverse Idioms with the General Chord Type (GCT) Encoding

The General Chord Type (GCT) provides accurate harmonic representation in the sense that it encompasses all the pitch-class-related information about chords. At the same time, for every pitch-class simultaneity, the GCT algorithm rearranges pitch-classes so that it identifies a root pitch-class and a chord “base” and “extension”, leading to chord representations that convey musical meaning for diverse musical idioms. The GCT representation has common characteristics with the stack-of-thirds and the virtual pitch-root-finding methods for tonal music, but has differences as well (Cambouropoulos et al., 2014). This encoding is inspired by the standard Roman numeral chord type labelling, but is more general and flexible. A recent study on the GCT representation indicated that it can be used both as a means to represent harmonic chords accurately, and to describe musically meaningful relations between different harmonic labels in diverse and not necessarily tonal musical idioms (Cambouropoulos et al., 2014; Kaliakatsos-Papakostas et al., 2014b; Cambouropoulos et al., 2015).

The GCT algorithm computes, for a given multi-tone simultaneity, the “optimal” ordering of pitches such that a maximal subset of consonant intervals appears at the “base” of the ordering (left-hand side) in the most compact form; the rest of the notes that create dissonant intervals to one or more notes of the chord “base” form the chord “extension”. Since a tonal centre (key) is given, the position within the given scale is automatically calculated. Input to the algorithm is the following:

• Consonance vector: a Boolean 12-dimensional vector is employed, indicating the consonance of pitch-class intervals (from 0 to 11). For example, the vector $[1,0,0,$ $1,1,$ $1,0,$ $1,1,$ $1,0,0]$ means that the unison, minor and major third, perfect fourth and fifth, minor and major sixth intervals are consonant. Dissonant intervals are the seconds, sevenths and the tritone; this specific vector is referred to in this text as the tonal consonance vector.
• Pitch Scale Hierarchy: this is given in the form of scale tones and a tonic. For example, a $D$ major scale is given as: $2, [0,2,4,5,7,9,11]$, or an $A$ minor pentatonic scale as: $9, [0,3,5,7,10]$.
• Input chord: list of pitch-classes (MIDI pitch numbers modulo 12).

For instance, the tonic chord is labelled as $[0, [0, 4, 7]]$, where the first occurrence of 0 denotes the root of the chord in relation to the scale’s tonic, and the base $[0, 4, 7]$ denotes the maximally consonant setup of the included pitch-classes. In relation to the tonal naming of chords, type $[0, 4, 7]$ is a major chord. Similarly, the dominant seventh (inverted or not) is labelled as $[7, [0, 4, 7], [10]]$, where there is a third element, $[10]$, which is an extension, i.e., an existing pitch-class that cannot be inserted in the maximally consonant set. The compressed GCT form will sometimes be used in this article where no intermediate brackets are used, e.g., $[7, [0, 4, 7], [10]]$ will be denoted as $[7\ 0\ 4\ 7\ 10]$. An example taken from Beethoven’s Sonata No.14, Op.27-2 illustrates the application of the GCT algorithm for different consonance vectors (Fig. 2). For the tonal vector, GCT encodes classical harmony in a straightforward manner. This way we have an encoding that is analogous to the standard Roman numeral encoding (Fig. 2, “tonal”). If the tonal context is changed to a chromatic scale context and all intervals are considered equally “consonant” i.e., all entries in consonance vector are 1s, we get the second “atonal” GCT analysis (Fig. 2, “atonal”) which amounts to normal orders (not prime forms) in standard pc-set analysis. In pitch-class set theory, normal orders do not have “roots”, however, they do have transposition values (T0-T11) in relation to a reference pc (normally pc 0); the normal orders with transposition values of pc-set theory are equivalent to the GCT for the “atonal” consonance vector.

An additional fundamental concern of the harmonic representation in the presented harmoniser is the grouping of chords according to their GCT representation with a methodology described in Kaliakatsos-Papakostas et al. (2015). For example, the V chord in a scale can be expressed either as $[7,$ $[0,4,7]]$ or in a “reduced” ($[7,[0,4]]$) or an “expanded” version ($[7,$ $[0,4,7,10]]$) that actually represent the same chord label. Each GCT group includes the GCT types that satisfy the following three criteria:

1. They have the same scale degree root.
2. Their GCT are subset-related.
3. They both contain notes that either belong (or not) to the given scale.

Regarding criterion 2, two bases $B_1$ and $B_2$ are considered subset-related if $B_1 \subseteq B_2$ or $B_2 \subseteq B_1$, e.g., $[0,4] \subseteq [0,4,7]$ while $[0,4] \not\subset [0,3,7]$. Criterion 3 is utilised to identify and group together chords that belong to secondary tonalities within the primary tonality of the piece. For instance, in a diatonic major context, while $c_1=[0,[0,4,7]]$ and $c_2=[0,[0,4,7,10]]$ fulfil criterion 1 and 2, according to criterion 3 they are not grouped together since $c_2$ includes value 10, which is mapped to the non-diatonic 10 pitch-class value. In a major context $[0,\ [0,\ 4,\ 7,\ 10]]$ is secondary dominant to the IV (V/IV) and is differentiated from the I major chord.

Furthermore, each group is represented by an “exemplar” GCT type, which is the one that is more often met in the datasets under study. Some common chord groups in the major scale Bach chorales are illustrated in Tab. 1. This table also includes the functional naming of each group in order to assist the comparison of the derived GCT types with the standard Roman numeral labelling. Testing this simple algorithm on sets of both major and minor Bach chorales gives a reasonable first classification of the “raw” GCTs. Groups of GCT chords are extracted from datasets and their exemplars are used to train the system.

3.2 Training Data and Harmony Annotations

The development of the presented melodic harmoniser incorporates statistical learning on different harmonic levels (chord transitions, cadences and voice-leading) from a data pool with “real-world” representations of historical traditions of music creation. By employing rich multi-level structural descriptions of harmony in different idioms, the harmoniser is able to create new music that accurately reflects the characteristics of these idioms. A diverse collection of musical pieces drawn from different historic eras and from drastically different harmonic styles have been assembled. Each idiom/style is as internally coherent as possible such that regularities of the specific harmonic space can be extracted; the idioms among them are as different as possible on all the examined harmonic levels. Additionally, the musical pieces are manually annotated such that structural harmonic features may be extracted at various hierarchic levels. Specifically, the following structural aspects are manually annotated: (a) harmonic reduction(s) of each musical work/excerpt so that structural harmonic/non-harmonic notes are explicitly marked, (b) local scale/key changes are determined so that harmonic concepts relating to modulations can be learned, and (c) grouping structure is given so that cadential patterns at various hierarchic levels can be inferred.

The required types of information from a music piece for training the system are illustrated in Fig. 3, and annotated music files include: (a) the original musical data (the actual musical surface), and (b) expert annotations that are provided as manually entered analytical information about the contents. At the lowest level of the musical surface (denoted as ms_0), which is the actual notes of a musical piece and the lowest level of representation that has musical significance (Jackendoff, 1987), a custom text-based encoding is used. Expert annotations in a music piece describe musicological aspects that refer to specific analytic concepts (e.g., the use of harmonic symbols to describe note simultaneities, modulations, phrasing, etc.). Specifically, the expert annotations include time-span reduction of the original content (ms_1) and annotations concerning tonality (and tonality changes) and grouping information.

On the chord transitions level the system is trained according to the chord progressions on the harmonic reduction (ms_1), with chords being encoded in the General Chord Type (GCT) representation (Cambouropoulos et al., 2014). Since the GCT requires tonality information, the GCT forms of the extracted chords are computed by using the tonality annotations. Annotations of groupings indicate the positions of cadences, where the system learns the final pair of chords before any group ending. Even though a cadential form may incorporate more or less than two chords, considering the last two chords of a phrase as a cadence was decided as a rational compromise.

The indicators of tonality – and tonality changes – include accidentals in chordal form, with all the included notes indicating an octave of the utilised scale (lowest note is the tonality’s fundamental), while the time instance of a tonality activation/change is defined by the indication’s onset. Additionally, it has to be noted that at least one tonality indicator at the beginning of the piece is required otherwise the tonality annotations of the piece are considered absent (repetitions of the same indicator are ignored). The grouping part contains annotations about melodically coherent temporal regions of the music surface. At the beginning of each phrase, a group identifier is placed indicating the level of the phrase hierarchy. One note on the lowest line indicates the lowest level groupings (e.g., phrase); two notes on the lowest two lines indicate an immediately higher-level of grouping (e.g., period); three notes indicate even higher level of grouping and so on. The cadences (i.e., the final pair of chords at the end of each grouping part) of each grouping level are learned separately.

The dataset consists of over 430 manually annotated musicXML documents categorised in seven sets and various subsets. The sets are categorised by genre, while subsets are created within genres that present notable differences in their harmonic structure. For instance, the chorales of Bach and jazz music belong to different sets, while modal jazz pieces belong to a different subset from jazz standards that incorporate tonality transpositions. The diversity in harmonic features among different sets and subsets allows the inclusion of a wider spectrum of options, enabling the melodic harmoniser to produce harmonisations with strong references to diverse idioms. Also, there is inner-idiom consistency in each subset, which is determined by “patterns” in harmonic features that are characteristic to this subset.

The dataset comprises seven broad categories of musical idioms, further divided into sub-categories, presented in the following list⁽¹⁾:

1. Modal harmonisation in the Middle Ages (11th–14th centuries): includes subsets of medieval pieces in the Organum and Fauxbourdon styles.
2. Modal harmonisation in the Renaissance (15th–17th centuries): includes modal music from the 16th–17th centuries along with modal chorales.
3. Tonal harmonisation (17th–19th centuries): includes a set of the Bach chorales, the Kostka-Payne corpus⁽²⁾ and tonal harmonisation sets from the 18th–19th centuries.
4. Harmonisation in National Schools (19th–20th centuries): includes 19th–20th century harmonisation of folk songs from Norway, Hungary and Greece.
5. Harmonisation in the 20th-century: includes harmonisations of Debussy, Hindemith, Whitacre, Stravinsky and Schnittke among others.
6. Harmonisation in folk traditions: includes Tango (classical and nuevo styles), Epirus polyphonic songs and Rebetiko songs.
7. Harmonisation in 20th-century popular music and jazz: includes mainstream jazz, pieces from Bill Evans and a collection of songs from The Beatles.

For the harmonisation examples incorporated in the present article, a subset of eight harmonic idioms were used from the dataset, listed below:

1. The 15th-century Fauxbourdon style, based on parallel $^6_3$ chords.
2. Modal homophonic style of the 16th/early 17th-century, mainly as encountered in Palestrina’s Stabat Mater.
3. The homophonic tonal harmonic idiom of J.S. Bach chorales.
4. The Kostka-Payne corpus, describing mainstream tonal harmony of the 18th/19th-centuries (Kostka & Payne, 2004).
5. Edvard Grieg’s 19th-century chromatic harmonic idiom, as expressed in his folksong harmonisations Op. 17 & 63.6.
6. The Epirus polyphonic singing style, based on the minor pentatonic scale (Lolis, 2006; Kaliakatsos-Papakostas et al., 2014).
7. Yannis Constantinidis’s 20th-century modal style, as encountered in his 44 Greek Miniatures for Piano (Tsougras, 2010).
8. Paul Hindemith’s 20th-century harmonic idiom, as expressed in his Six Chansons.

3.3 Melodic Input

After the system is trained, it is able to harmonise a given melody. Fig. 4 illustrates an instance of the input protocol for the system, which includes the melody to be harmonised and information regarding some harmonic attributes that are not inferred by the system at this stage. The input melody, at this stage, is manually annotated to indicate harmonic rhythm, harmonically important notes, tonal centre, and phrase structure. The file that produced this figure is used as input for harmonising the example in Fig. 7 (b). Initially, the user provides the positions where chords should occur (harmonic rhythm), as well as the important notes (harmonic notes) that should be considered when selecting chords for each segment. If the user provides no information for these attributes, the system produces default harmonic rhythm and important note selection schemes that might lead to “unwanted” harmonic results. Additionally, the user has the freedom to choose specific chords at desired locations (constraint chords), forcing the system to creatively produce chord sequences that comply with the user-provided constraints, therefore allowing the user to “manually” increase the interestingness of the produced output. Finally, the user should accompany the melody with higher level harmonic information concerning the tonality or tonalities of the piece, as well as with its phrase grouping boundaries. Tonality is indicated by a cluster of all notes included in the scale describing the tonality, with the lowest note indicating the tonality’s tonic. Grouping is annotated by arbitrary notes at the metric position where grouping changes occur, while the number of notes in these positions indicate the grouping level of the phrase.

Why is tonality among the features that are imported by the user along with the melody? Although speculations about the local tonality of a melody could be automatically deduced algorithmically (Chai, 2005; Kaliakatsos-Papakostas et al., 2013), manual annotation of tonality and changes has been decided for the following reasons:

1. Utilisation of non-standard (major/minor) tonalities: the collected dataset includes pieces that do not conform to the standard Western Music tonalities, e.g., there are pentatonic or octatonic modes. Additionally, the user is allowed to insert any desirable tonality, which will lead the system to select the “proper” set of chords to harmonise the given melody.
2. Accuracy in tonality-change boundaries: algorithms that perform melodic segmentation according to tonality are not able to identify the exact location of tonality boundaries. For the presented melodic harmoniser, it is important that the tonality (and phrase level) change locations stay aligned with the melody segments that a human user indicates.
3. The ability to insert “subtle” tonalities: the user is able to introduce tonality changes in places where an algorithm might not identify any change. This ability introduces additional agility and potential to the system.

In the training data, tonality changes are treated differently in different idioms while, additionally, some idioms do not include (or include very specific) modulations between certain – neighbouring in the circle-of-fifths – tonalities. Since modulations are dependent on the melody, and a user-input melody might incorporate arbitrary modulations, it is clear that no learning strategy on every idiom could cover the entire spectrum of modulations that are possible for input melodies. For instance, in the idiom of modal music there are no modulations, since entire pieces are composed in a single mode. Therefore, it would be impossible to harmonise a melody that incorporates tonality modulations using the harmony of a modal idiom, since no training paradigms would be available for such a task. For the purpose of the “idiom independent learning” that is required for the presented system, modulations are not tackled: a cadence of the first tonality is assigned before the modulation occurs and the material after the modulation is treated as a new phrase in the new tonality.

4 Chord Progressions, Intermediate Constraints and Cadences

The core of the generative process is the production of GCT chord progressions with a probabilistic methodology that is a simple extension of the Hidden Markov model (HMM) method that allows the inclusion of fixed “anchor” chords. Harmonisation with fixed anchor chords is considered a crucial component of the presented work, since it enables the prior definition of important chords in intermediate positions of the melody to be harmonised. Two types of important chords are considered: intermediate or final cadences at positions where phrases end, and user-defined fixed chords that the system is forced to use. For the pieces used to train the system, the format of which is described in Section 3.2, annotations about phrase boundaries are also included. During training, the final pair of chords (penultimate and final chord) in each phrase is independently stored in the cadence module of the system, wherein the probabilities of intermediate and final cadences are calculated. Except from the indicated positions of phrase endings, the user is also able to assign specific desired chords at any desired position, directly allowing the involvement of the user’s creativity in the harmonisation prosess. Both the phrase ending positions and the user-defined chords are included in the directions provided by the user in the melody input file, as described in Section 3.3. These chords act as “anchors” that remain fixed for the constrained HMM (cHMM) (Kaliakatsos-Papakostas & Cambouropoulos, 2014) algorithm that selects “proper” chord sequences connecting the intermediate parts of the fixed chords, under the conditions introduced by the melodic material to be harmonised. The results presented in Kaliakatsos-Papakostas & Cambouropoulos (2014) indicate that cHMMs produce harmonisations that are potentially completely different to the ones produced by HMMs, depending on the imposed constraints.

4.1 Probabilistic Generation of Chord Progressions with Intermediate Constraints

The proposed harmoniser uses the cHMM (Kaliakatsos-Papakostas & Cambouropoulos, 2014) algorithm for generating chord progressions. The aim of this algorithm is to preserve the merits of probabilistic harmonisation, i.e., ability to train on different idioms and flexibility in generation, while allowing prior determination of intermediate chords (also referred to as checkpoints in the literature, see Chuan & Chew (2007)). Such constraints in the context of Markov chains (with no demands imposed by observations) are also known as “unary” constraints (Pachet et al., 2011), however the cHMM algorithm works under the assumption sequences of states (chords) are composed given a set of observations (melody). Allowing fixed intermediate chords introduces two advantages for the presented harmoniser: (a) the preservation of higher level harmonic structure by the imposition of intermediate and final cadences, and (b) the interactivity with the user by allowing any desired chord to be placed at any position. In the case of the cadences, the intermediate chords that compose the cadence are specified by a probabilistic algorithmic process described later, that captures statistics about cadence occurrences either in intermediate phrase ending or at the end of the piece, allowing the learning of music structure on a higher hierarchical level. Direct human intervention on selecting desired chord constraints in the cHMM algorithm allows the presented harmoniser to function as a melodic harmonisation assistant that allows its user to specify a harmonic “spinal chord” of anchor chords that are afterwards connected by chord sequences that give stylistic reference to a learned idiom. Such an assistant could be valuable for both creative harmonic experimentation and, potentially, for educational purposes.

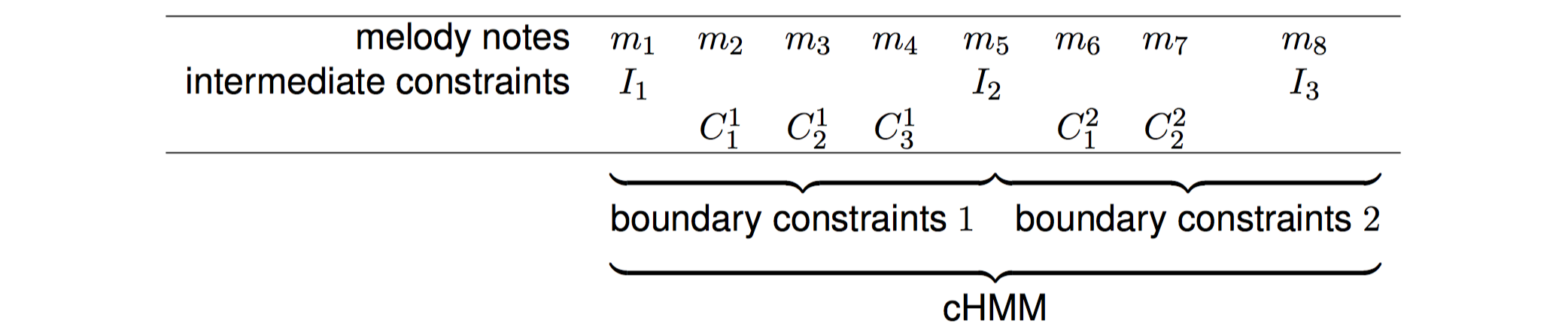
The cHMM methodology divides the problem of finding intermediate constraints into several consecutive problems of finding boundary constraints i.e., fixed beginning and ending chords. Tab. 2 illustrates this process, where the intermediate chord constraints ($I_j$) are preserved while new chords ($C_i^j$) are generated, given the melody notes ($m_i$). The problem of assigning intermediate chord constraints is transformed into the problem of finding consecutive beginning and ending chords for each intermediate segment. In Simon et al. (2008), the HMM variation that was presented included an additional layer of probability distributions for beginning and ending chords for harmonising a part. In the cHMM methodology, used in the presented harmoniser, the probability values in the distributions for beginning and ending chords in each intermediate segment are actually binary: the chord that is selected as constraint has probability value $1$, while all the others have $0$.

During the cHMM training phase, an initial set of musical phrases are considered, which provides the system with the required statistical background, constituting the training set. For the remainder of this section, the set of possible state-chords will be denoted by $\mathcal{S}$, while the letters $C$ and $c$ will be used for denoting chords. The set of all possible observation-notes will be denoted as $\mathcal{Y}$, while $Y$ and $y$ will denote melody notes. There are four factors the cHMM algorithm needs to generate a chord sequence, given a melody.

Three factors are induced by the statistics from the training set.

1. The probability that each state (chord) is a beginning chord. This distribution is computed by examining the beginning chord for each phrase in the dataset and is denoted as $\pi (C_1 = c)$, $c \in \mathcal{S}$.
2. The probability that each state (chord) is an ending chord. This distribution is computed by examining the ending chord for each phrase in the dataset and is denoted as $\tau (C_T = c)$, $c \in \mathcal{S}$.
3. The probability that each state follows another state, denoted as $P(C_i = c_i | C_{i-1} = c_{i-1})$, $c_i$, $c_{i-1}\in \mathcal{S}$. One additional “pseudo-distribution” is included, except from the beginning and ending chords and transition probabilities learned from data.
4. A vector assigning “pseudo-probability” values to chords that include the melody’s important notes for each chord segment, denoted by $P(C_i = c_i | Y_i = y_i)$. As presented in further detail in Section 3.3, a chord might be harmonising a phrase segment that includes more than one melody note, while the user is able to select which among the melody notes are important. For assigning a proper chord over a melody segment, the harmoniser tries to find chords that include as many of the important notes as possible. Thereby, for each melody segment to be harmonised by a chord, each chord is assigned a “pseudo-probability” value according to how many of the segment’s important notes it includes. Therefore, for a melody segment, chords that include more important melody notes are more probable.

The overall probability for selecting a chord in a segment of $T$ chords is computed by:

$$\begin{equation} P(C_i = c_i | Y_i = y_i) = P_\pi \ P_\mu \ P_\tau \text{,} \end{equation}$$ where $$\begin{equation} P_\pi = \pi (C_1 = c_1)\ P(C_1 = c_1 | Y_1 = y_1) \text{,} \end{equation}$$ $$\begin{equation} P_\mu = \prod_{i=2}^{T} P(C_i = c_i | C_{i-1} = c_{i-1}) P(C_i = c_i | Y_i = y_i) \text{,} \end{equation}$$ $$\begin{equation} P_\tau = \tau (C_T = c_T)\ P(C_T = c_T | Y_T = y_T) \text{.} \end{equation}$$

The generated sequence of chords is statistically optimal, in the sense that it presents a maximal combination for the probabilities in all the counterparts ($P_\pi$, $P_\mu$ and $P_\tau$), typically through the Viterbi-Forney (1973) algorithm. The probabilities in $P_\pi$ promote some chords as better solutions to begin the path of chords i.e., the ones that are more often used in the beginning of pieces in the dataset. Similarly, the probabilities in $P_\tau$ advance solutions that are more often met as concluding chords. However, in case the beginning and/or ending chord is a constrained chord, the $P_\pi$ and/or $P_\tau$ distributions respectively are becoming “binary”, promoting only the chord that has been selected as constraint (with probability value $1$). Specifically, if the beginning and ending chords are selected to be $\alpha_1$ and $\alpha_T$ respectively, the new probabilities that substitute the ones expressed by Equations 2 and 4 are the respective following:

$$\begin{equation} P_\pi^{'} = \left\{ \begin{aligned} [changed] & 1, \text{ if } C_1 = \alpha_1\\ & 0, \text{ otherwise} \end{aligned}\right. \end{equation}$$ $$\begin{equation} P_\tau^{'} = \left\{ \begin{aligned} [changed] & 1, \text{ if } C_T = \alpha_T\\ & 0, \text{ otherwise.} \end{aligned}\right. \end{equation}$$

4.2 Learning and Assigning Intermediate and Final Cadences

The limited memory according to the order of the Markov-based methods (Pachet et al., 2011) does not allow them to consider longer time dependencies, a fact that is necessary for reflecting hierarchical structure of harmony. The intermediate chord constraints, apart from allowing direct user-intervention in the generative process, allow for the preservation of harmonic information on a higher harmonic level, by employing intermediate and final cadences according to the phrase boundaries indicated by the user in the melodic input. Statistics for these cadences are learned during the training process (see Section 3.2), where expert annotated files including annotations for phrase endings are given as training material to the system.

Cadences are considered to be the final two chords of a phrase; during the cadence training process the two final chords in every phrase of every piece in the training data are captured. Statistics for unique cadences/pairs of chords are collected for two types of cadences:

1. Final cadences that are taken from the end of each piece’s final phrase.
2. Intermediate cadences that are taken from the ending of every non-final phrase in each piece.

The final cadences collected from a set of 31 Bach chorales – a well-known idiom – is demonstrated in Tab. 3, along with times they have been used. The set of final cadences collected from this set of Bach chorales reveals the specificity of cadential patterns in this idiom, including only variations of the perfect (and Picardy for the minor). The number of different intermediate cadences is not overwhelmingly larger: except for the perfect and imperfect cadences, there are also some occurrences of the plagal and interrupted cadences along with some isolated cadential schemes that appear rarely.

After collecting statistics about cadences from all idioms the system, before employing the cHMM algorithm, assigns cadences as fixed chords to the locations indicated by user-input (see Section 3.3). The cadence to be imported is selected based on three criteria: (a) whether it is a final or an intermediate cadence, (b) the cadence likelihood (how often it occurs in the training pieces), and (c) how well it fits with the melody notes that are harmonised by the cadence’s chords. Specifically, for an intermediate or a final cadence, cadence likelihoods are taken from the probability distributions of each cadence in an idiom i.e., how many times a cadence occurred over the total number of cadences. The appropriateness of a cadence according to the melody notes that the cadence’s chords harmonise, is measured for each chord separately with the same method used in the cHMM algorithm, however, if a cadence chord lacks at least one important note in the segment it harmonises, then the cadence is disregarded as a whole (pair of chords). If for a given phrase ending no complete cadence (as a pair of chords) is found, then only the final chords are determined. If the utilisation of solely the final chords fails again, then no constraint is assigned for the cHMM. The motivation behind this cadence rejection mechanism was the reflection of the notion that the selected harmonisation idiom does not include a phrase closure tool set for the notes of the melody in the location that the user indicated a phrase ending, or at the end of the piece.

5 Bass Voice-Leading and Voicing Layout of Chords

Experimental evaluation of methodologies that utilise statistical machine learning techniques demonstrated that an efficient way to harmonise a melody is to add the bass line first. This conclusion was made through the information theoretic measure cross-entropy, when the soprano, alto, tenor and bass voice were pairwise compared regarding their statistical relations. The proposed harmoniser uses a modular methodology for determining the bass voice-leading presented in Makris et al. (2015b), which includes independently trained modules that function on the previously defined GCT chords that constitute the harmonisation. These modules include (a) a Hidden Markov model (HMM) deciding for the bass contour (hidden states), given the melody contour (observations), (b) distributions on the distance between the bass and the melody voice, and (c) statistics regarding the inversions of the chords in the given chord sequence. The generation of chords (in GCT form) is performed by the cadence and cHMM probabilistic modules thus the selection of the proper voice layout scenarios for each GCT chord depends on the chords’ inversion probabilities. After the bass voice is defined, the voicing layout of the intermediate chord notes is fixed.

5.1 Defining Bass Voice Motion

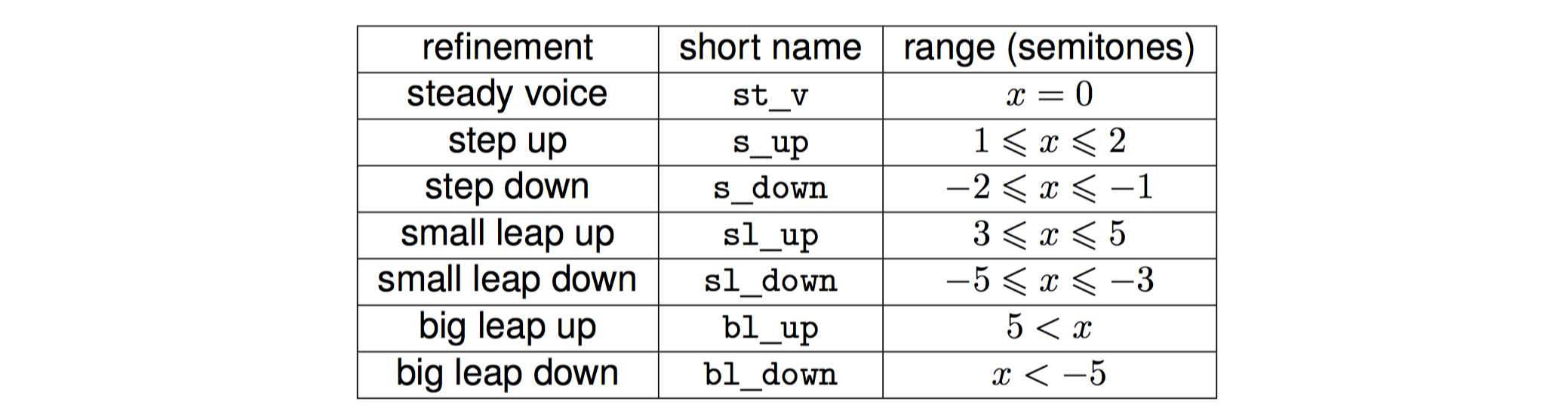
For constructing the bass voice-leading, it is assumed that the bass voice is both a melody itself and that it also depends on the piece’s melody, a fact that motivates the utilisation of HMM. The primary module for defining bass motion plays the role of the hidden states under the first order Markov assumption for bass contour (a bass motion depends on its previous one), in combination with observations of the melody’s contour (a bass motion depends on its motion). Both the bass and the melody voice steps are represented by abstract notions that describe general quantitative information on pitch direction, also called “direction descriptors”. In Makris et al. (2015a) several scenarios for voice contour refinement were examined, providing different levels of accuracy for describing the bass motion in different datasets. In the presented harmoniser, the melody and bass note changes are divided into seven steps, as shown in Tab. 4. The selected scenario of seven steps is based on the assumption that the perfect fourth is a small leap while the perfect fifth as a big leap.

The level of refinement for representing the bass and melody voice movement give us the number of states and observations. According to the HMM methodology, the training process incorporates the extraction of statistics about the probabilities that a certain state (bass direction descriptor) follows another state, given the current observation element (melody direction descriptor), independently of the chord labels. These statistics are extracted from the training pieces of each idiom and incorporate four aspects:

1. The probability for each bass motion to begin the sequence.
2. The probability for each bass motion to end the sequence.
3. The probability that each bass motion follows another (transition probability).
4. The probability of a bass motion to be present, given a melodic step.

The sequence of states that is generated by an HMM system is produced according to the maximum probability described by the product of the aforementioned statistics, given a sequence of melodic contour observations. The extracted probabilities for each possible next bass motion are stored in a vector of probabilities $\vec{p_m}$, which is afterwards utilised in the product of probabilities from all modules in Equation 7.

The bass voice motion provides abstract information about the motion of the bass, however, assigning actual pitches for a given set of chords requires additional information. Additionally, it might be the case that the best bass motion selected from the HMM module does not match other criteria concerning the chords that have already been selected by the cHMM, or the limits about permitted bass note pitch height. What if the best bass motion cannot be implemented for a chord, because it requires a rather rare inversion of this chord? What if the best bass motion drives the bass voice too high and close to the melody or too low? In order to assign a bass voice to a chord, additional information is required in the voice layout modules of the presented methodology, namely regarding inversions and the melody-to-bass distance. The inversions of a chord play an important role in determining how eligible to be a bass note a chord’s pitch class is, while the melody-to-bass distance captures statistics about the pitch height region that the bass voice is allowed to move within, according to the melody.

All inversions of a chord are obtained by assigning each of its pitch-classes a bass note. For instance, the chord with pitch-classes $[0,4,7]$ has three inversions, with each one having a bass note that corresponds to a different pitch-class. The voicing layout module of the harmonic learning system regarding chord inversions is trained through extracting relevant information from every (GCT) chord, in every piece, from each musical idiom. For mapping pitch-class related inversion information directly to GCT chords, a GCT chord is considered in the form $g = [r,\ \vec{t}]$, where $\vec{t}$ is the vector describing the type of chord, i.e., its base and extension in one array. For instance, the V chord in a key is expressed as $g = [7,\ [0,4,7,10]]$ in the GCT representation, where 4 denotes the major third, 7 the perfect fifth, and 10 the minor seventh. Under this context, the GCT type is a set of integers, $\vec{t}$ $=[t_1,\ t_2,\ \dots \ ,\ t_n]$, where $n$ is the number of type elements that can be directly mapped to relative pitch-classes (PCs). The statistics concerning chord inversion are expressed as the probability ($p_{\text{i}}$) that each type element in $g$ is the bass note of the chord, or

$$ p_{\text{i}} = (v_1,\ v_2,\ \dots \ ,\ v_n) \text{,} $$

where $v_i$, $i\in \{1,2,\dots ,n\}$, is the probability that the element $t_i$ is the bass note. Tab. 5 shows the extracted statistics for inversions for the most common chords found within Bach chorales. Therein it can be observed that these chords are more often met in root position, while they are rarely played in the second inversion (fifth as bass note). Therefore, by integrating the inversion probabilities ($p_{\text{i}}$) with in the voice layout modules as described in Equation 7, the second inversion of the $[7,[0,4,7]]$ chord would be avoided when harmonising in the style of the Bach chorales, since the probability related to its fifth being the bass note is zero.

An additional important aspect of voice layout is the absolute range of chords in the chord sequences of an idiom, or, the absolute difference between the bass voice and the melody. Different idioms encompass different constraints and characteristics concerning this voicing layout aspect according to several factors, one being the utilised instruments’ range. For capturing the distances between melody and bass pitch height in an idiom, interval-related information is extracted as approximate indicators about the expected pitch height of the bass voice through histograms of all melody-to-bass intervals found in the idiom’s training pieces. Since exact intervals are scale-sensitive – for example different scales can potentially produce different distributions of melody-to-bass intervals – the “expected” bass pitch height is approximated by a normal distribution (denoted by $p_{h_{x}}$) that is adjusted to fit the distribution of the melody-to-bass intervals observed in the dataset.

For defining the pitch value of the bass in every step, the probabilities gathered from all the modules described hitherto are combined into a single value, computed as the product of all the probabilities from all the incorporated modules. To this end, for each GCT chord ($C$) in the sequence composed by the cHMM and cadence modules, every possible scenario of chord inversions and bass note pitch height, denoted by an index $x$, is generated. For each scenario ($x$), the product ($b_{x}(C)$) of all the modules discussed so far is computed i.e., the bass motion ($p_{m_{x}}(C)$), the inversions ($p_{i_{x}}(C)$) and melody-to-bass interval ($p_{h_{x}}(C)$):

$$\begin{equation} b_{x}(C) = p_{m_{x}}(C)\ p_{i_{x}}(C)\ p_{h_{x}}(C) \text{.} \end{equation}$$

Therefore, the best scenario ($x_\text{best}$) for the bass voice of chord $C$ is found by: $x_\text{best} = \operatorname*{arg\,max}_x (b_{x}(C))$.

It has to be noted that the bass note motion probability ($p_{m_{x}}(C)$) of all examined inversions and pitch heights is obtained by the HMM module and takes a value given by the vector $\vec{p_m}$ according to the bass step it leads to. Therefore, the HMM probabilities are not utilised to compute the best sequence of all bass motions throughout the harmonisation i.e., with the Viterbi algorithm. Contrarily, for the bass motion that is currently examined, all seven probabilities are calculated and stored in $\vec{p_m}$, while all possible pitch heights of the current chord (indexed by $x$) are assigned with a probability value accordingly. It should also be noted that the exact pitch height of the first bass in the first chord is calculated without information from the bass motion module ($p_{m_{x}}(C)$) since there is no motion in the bass before that.

An additional adjustment concerning the melody has to be made to avoid “mistakes” in the selection of the optimal bass pitch height that are caused by potential steep leaps in the melody. For instance, a given melody may at some point move suddenly to very high pitches and then return to its former pitch region. The effect of the melody-to-bass distribution would be to “drag” the bass notes and make them follow the melody, producing a bass motion that sounds unnatural to most tested idioms. To this end, the melody line is “smoothed” with a moving average of ten positions i.e., every pitch height in the melody is substituted by the mean value of its ten previous pitch heights (or fewer than ten, for melody notes before the 10th)

5.2 Defining Chord Notes Between the Bass and the Melody

Obtaining the best scenario for bass voice-leading determines the exact pitch value of the bass voice for each GCT chord according to the bass motion HMM, inversions of the given GCT chord and the distance between the bass voice and the soprano. Depending on the number of notes in each GCT, the voicing layout, i.e., exact pitches for all chord notes, for each chord has to be defined. To our knowledge, no study exists that focuses on examining the position of inner voices inside a generated chord. Therefore, a simple statistical model is proposed that utilises a generic tree data structure to find the best combination of the intermediate voices for every chord according to some simple criteria. Our proposed methodology is summarised as follows:

1. Find all the possible combinations of the intermediate notes and store them in a generic tree structure.
2. Calculate the cost for every combination and select the best.

The total cost of every combination, in turn, is based on a weighted combination three cost criteria:

1. Proximity to a pitch-attractor: the combination that best matches this criterion is the one that incorporates inner voice pitch values that are closer to a certain pitch value, named the pitch-attractor. The pitch-attractor value is set to a fixed ration between the bass and the lowest melody note in the block of each chord.⁽³⁾
2. Evenness of neighbouring note distances: evenness in inner voices of a chord is measured by calculating the standard deviation of their pairwise distances.
3. Inner voice movement distances between chords: the inner voice movement between the previous and the current chord is calculated as the mean value of distances between the highest and the lowest inner voices. The best chord according to this criterion is the one with highest and lowest intermediate note pitches that are closest to the respective ones of the previous chord.

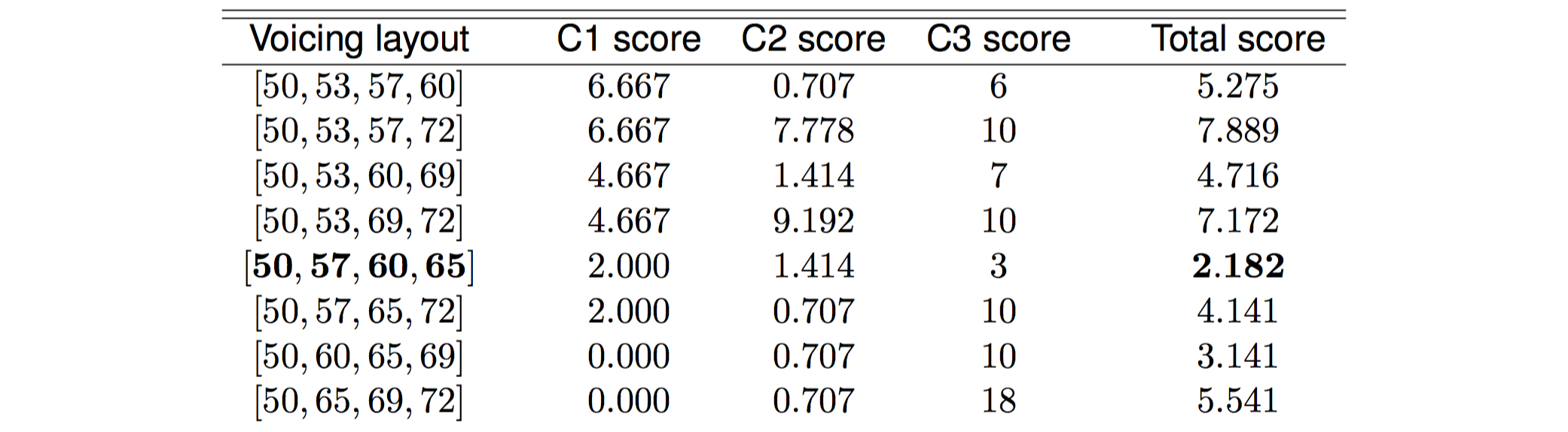
After thorough examination of the results in many simulations, the weight of the cost criteria are respectively: $0.5$, $0.2$ and $0.3$. The voicing layout that is selected is the one that achieves the lowest total score in the weighted cost combination value.

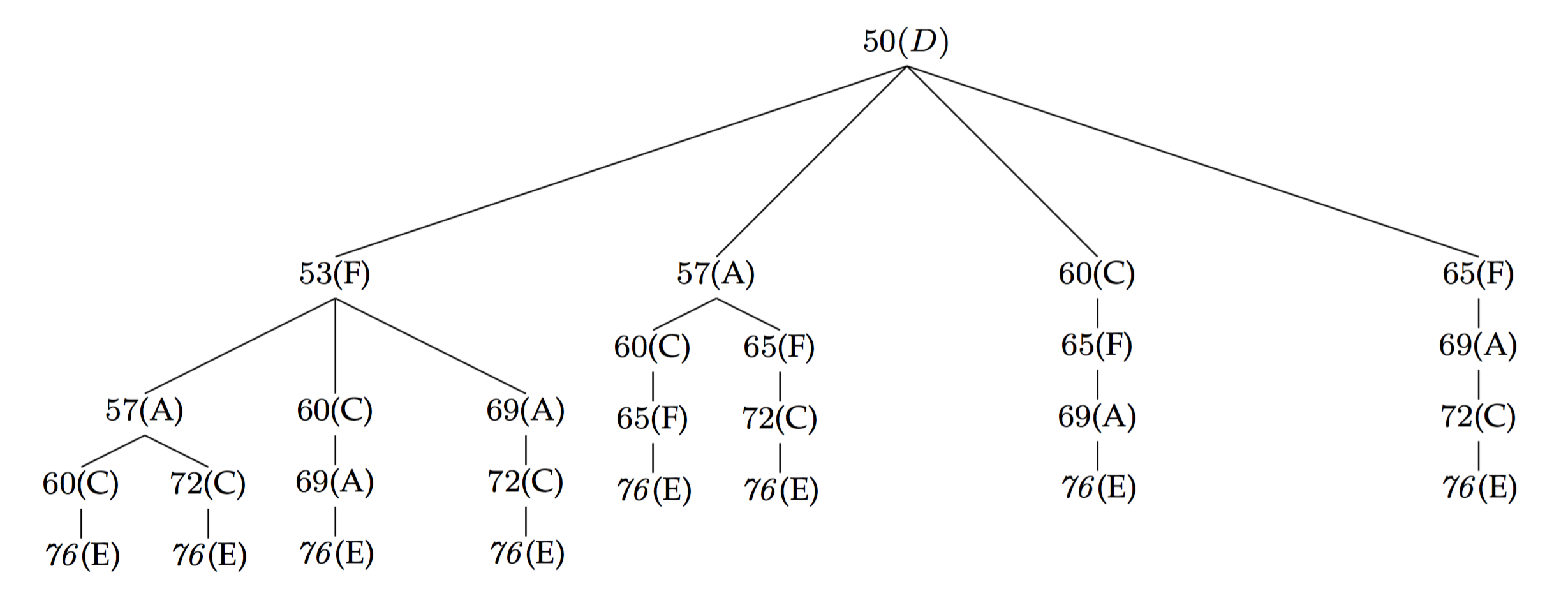
For example, consider that the GCT chord currently examined is $[2\ 0\ 3\ 7\ 10]$ with pitch-classes $[0,2,5,9]$ (D minor seventh), while the previous chord was the GCT chord $[0\ 0\ 4\ 7]$ (C major). Consider also that the chord’s MIDI pitches are $[48,55,64]$, where the melody note is not considered, i.e., $55$ and $64$ are the inner notes of this chord, while for the D minor seventh, the bass note value calculated by Equation 7 is $50$ and the current melody note is $76$. There are many possibilities for arranging the current chord’s (D minor seventh) inner notes. To this end, the generic tree structure illustrated in Fig. 5 is generated such that it represents all the voicing layout possibilities. All possible voicing layouts are taken by the tree by descending each branch from the root and they are then evaluated according to the three aforementioned criteria, the results of which are shown in Tab. 6.

6 Experimental Results

The creative and structural characteristics of the system are examined through presenting examples on different harmonisation tasks as well as through statistical measures of similarities in harmonisations of melodies with different learned harmonies. The melodic harmonisation examples concern five melodies as well as different structural harmonisation attributes, e.g., intermediate phrase boundaries and user-selected chord constraints. These examples demonstrate the system’s potential and indicate the integrity of harmonisations that, in some cases, reach human expert-standards with minor adjustments

The statistical experimental process (presented in Section 6.2) examines the similarity between system-generated harmonisations of (11) different melodies and original training harmonisations. This process reveals that the harmonisations produced by the system when trained on an idiom may diverge from that idiom, depending on how its harmonic characteristics align with the structural properties and implied harmony of input melodies.

6.1 Example Harmonisations

Five diverse short melodies were chosen, three from classical music (baroque, classical and romantic periods), one popular song and one folk song:

1. J.S. Bach: the fugue theme from the Well-Tempered Clavier I, Fugue No. 8 transposed to D minor. The melody is a 3-bar phrase that concludes with a perfect cadence in D minor.
2. L.V. Beethoven: the melodic theme (bb. 1–8) from the second movement in A$\flat$ major of the Piano Sonata No. 8. The melody comprises two 4-bar phrases (imperfect cadence to perfect cadence) that form an 8-bar period.
3. The Beatles: the first melodic phrase of the song “Michelle”, transposed to C minor. It is a 6-bar phrase, ending with an imperfect cadence to the dominant.
4. Greek folk song: “Tou Kitsou &emacr mana”, taken from Yannis Constantinidis’s collection 44 Miniatures for Piano (No. 27). The melody is in A dorian mode, and comprises two phrases (4-bar and 7-bar) of which the second consists of two sub-phrases (3-bar and 4-bar).
5. Gabriel Fauré: the first three phrases (bb. 2–21 without the repetitions) of the Sicilienne for cello and piano (Op. 78). The melody is mainly in the dorian mode; the first two phrases form an 8-bar period (imperfect cadence to perfect cadence), while the third phrase exhibits tonal/modal mixture.

Eight different musical idioms (see Section 3.2) were used for the harmonisation of the above melodies, rendering twelve harmonisation examples. The system produced raw midi files that were processed by humans using the Finale 2014 musical notation software.⁽⁴⁾ The process involved the following: correction of musical notation issues and enharmonic spellings of pitches, separation of the bass line in a different layer or staff, preservation of constant number of active voices in the musical texture through the use of octave doublings, manual arrangement of the inner voices for smoother voice-leading where needed, and analysis of harmonic progressions through the use of Roman numeral notation in cases of tonal harmonisation. The pitch content of chords were always kept intact, and the bass line was manually altered in very few cases (indicated by* in the scores) in order to avoid stylistic inconsistencies or achieve better voice-leading.

The Bach fugue theme was harmonised three times (see Fig. 6), without the use of chord constraints. The first harmonisation was based on the Kostka-Payne corpus (classical/romantic tonal harmony), which is compatible with the style of the melody, and is characterised by frequent use of the dominant and a chromatically embellished perfect cadence prepared by two chords with pre-dominant function: ii$^{6}_{5}$ and vii$_o^7$ of V. The second harmonisation uses the Epirus polyphonic singing style and is almost consistently based on the D minor pentatonic scale (D, F, G, A, C) with the E of the last bar being the only exception. The chords are mildly dissonant verticalisations of the pentatonic set instead of the D minor triad, which – typically in this idiom – was avoided, and there is also a constant drone of the pitch centre in the lower voice. The third harmonisation was made in the Hindemith style and exhibits free mildly dissonant chords, mostly free verticalisations of diatonic sets, except from the cadence which is tonal (V$^2$ - I$^6$). Interestingly, pitches not included in the scale of the melody are inserted for the creation of idiomatic harmony, such as B, F$\sharp$ and C$\sharp$.

The Beethoven theme was harmonised three times (see Fig. 7). The first one (without chord constraints) was based on the Kostka-Payne idiom and is quite close to Beethoven’s own style, particularly in the second phrase, which incorporates progressions in the circle-of-fifths and a perfect tonal-cadence. However, the proposed harmony of the first phrase was considered static due to an insistent use of the V$^7$-I progression, so a second harmonisation based on the same idiom was attempted, albeit with two chord constraints in the first phrase (indicated by rectangular frames in the score). The result is substantially different, and the “chain” reactions caused by the injected chords expel the tonic chord completely from the first phrase and create interesting chromatic tonicizations and an imperfect cadence in the phrase’s end. The theme’s third harmonisation used the highly chromatic Grieg idiom and rendered even more daring and interesting chromatic chords, such as the altered dominants with lowered fifths (b. 2 and 4, French-type augmented 6th chords), the borrowed viio7/Vvii$^{o7}$/V with the tonic pedal note in the third voice (b. 3), the tonal mixture chords $^\flat$VI and $^\flat$III (bb. 5 and 6), of which the $^\flat$VI is doubly altered, and the German-type augmented sixth chord preparing the ii$^7$ chord (bb. 6 and 7).

The Beatles melodic phrase was harmonised twice (see Fig. 8), both without any chord constraints. The first harmonisation followed the Bach chorale idiom and rendered typical diatonic or chromatic tonal progressions leading to an anticipated imperfect cadence to the dominant. The second harmonisation was based on Yannis Constantinidis’s 20th-century modal idiom, and featured almost exclusively freely used major triads with major sevenths and minor triads with a minor seventh. In this rendering, interesting parallel harmony elements are observed (A$\flat^{\text{maj}7}$-Gm$^7$-Fm$^7$-E$\flat$m), while the imperfect cadence is avoided and substituted by a III chord with a major seventh. Two bass notes were manually changed (indicatedby *s) in order to create a complete stepwise descent from A$\flat$ to C in the bass line.

The Greek folk song was harmonised four times (see Fig. 9), all without any chord constraints. The first was based on the Fauxbourdon medieval idiom, characterised mainly by parallel $^6_3$ chords and cadences to open eight-fifth sonorities. The system proposed suitable chordal content (major or minor triads, open-fifth and one diminished triad as penultimate cadential chord), but the bass line had to be manually changed six times in order to achieve stylistic compatibility. The second harmonisation was produced from the homophonic modal idiom of the late 16th/early 17th-century. Interestingly, the proposed chords are mainly seven freely used major triads whose roots are connected through the circle-of-perfect-fifths: B$\flat$-F-C-G-D-A-E, while only one minor triad is used (A minor). Three manual adjustments were performed in the bass line to avoid $^6_4$ sonorities. The third harmonisation moves the harmonic style forward by one century, and is based on Bach chorales. The result is tonal functional harmony, with diatonic and chromatic elements (tonicizations) and with tonal cadences at the end of the phrases and sub-phrases. The proposed bass line was left intact, in spite of the awkward augmented second in the first bar. The last harmonisation is based on Hindemith’s harmonic idiom, and is characterised by free use of chromaticism, mildly dissonant sonorities stemming from diatonic sets and more stable sonorities (major or minor triads) at the end of the phrases (a notably interesting progression is the transition from Em$^7$ to Gm at b. 6-7).

Finally, two harmonisations of the Sicilienne melody are illustrated in Fig. 10. The first was based on the jazz harmonic idiom, characterised mainly by the free use of seventh chords and other extended/chromatic chords. The proposed harmony is a mixture of tonal and modal jazz harmony, with free chromatic or diatonic modal chords encountered during the unfolding of the melody and more tonal/functional progressions at the cadences. The second harmonisation was based on Hindemith’s neotonal, mildly dissonant, non-functional harmony. The free chromaticism employed produced interesting enharmonic phenomena (e.g., at b. 9 and 11).

Overall, the twelve harmonisations of the five chosen melodies produced by the system with some unobtrusive human manipulation incorporated a wide spectrum of musical idioms – with a range of over eight centuries – and demonstrated the flexibility and creative potential of the proposed harmonisation system.

6.2 Statistical Similarities Between Original Harmonies and New Melodic Harmonisations

The system is trained on several statistical aspects of a specific idiom and it uses the learned material in input melodies to produce novel harmonisations. How similar are the produced harmonisations in relation to the original training harmonisations of an idiom? In other words, is the system only able to mimic the training harmonisations or it is possible that “divergent” harmonisations can be produced? This question is addressed by examining the statistical similarities between original harmonies of idioms and harmonisations produced by the system for several melodies. The melodies used for producing harmonisations for this study include the five of the examples presented previously (one major and four minor melodies), with the addition of five major mode and one minor mode melodies, to compile a total set of six major and five minor melodies. The set of major melodies includes melodies from Haydn, Mozart, Beethoven, Jobim and two traditional ones, while the selected minor melodies are by Bach, “Michelle” by the Beatles, Sicilienne by Fauré and two traditional melodies.

The statistical similarity of harmonies in this experimental process is based on the transitions of GCT chords. Voicing layout elements are disregarded for this study since their complex statistical interdependence makes it hard to construct a unique statistical model that can be used for statistical similarity. Instead, this study examines similarities of GCT chord transition probabilities in original pieces (used for training the system) and novel harmonisations. The examination concerns one idiom at a time, $\mathcal{I}$, where the available training harmonies (pieces with more than four-chord transitions) are considered to form a set $\mathcal{T_\mathcal{I}}$, while the harmonies produced by the system for new melodies form the set $\mathcal{M_\mathcal{I}}$. Each harmonic piece in both sets is represented by its first-order Markov transition matrix, which represents its GCT chord transition probability distribution.

The distance between two transition probability distributions is quantified by the Hellinger distance (Gibbs & Su, 2002), which is a distance metric for two distributions. Using this metric a pairwise distance matrix is constructed for both the original $\mathcal{T_\mathcal{I}}$ and the generated $\mathcal{M_\mathcal{I}}$ harmonic pieces for each idiom ($\mathcal{I}$). This matrix is mapped afterwards into a two-dimensional space using multidimensional scaling (MDS), in order to obtain a Euclidean approximation of the space of GCT chord transition distributions based on their pairwise distances. Two major and two minor-mode examples of the two-dimensional spaces produced by this process are presented in Fig. 11, where the sets $\mathcal{T_\mathcal{I}}$ (grey $\times$s) and $\mathcal{M_\mathcal{I}}$ (red circles) for the Bach chorales and the Kostka-Payne sets are illustrated.

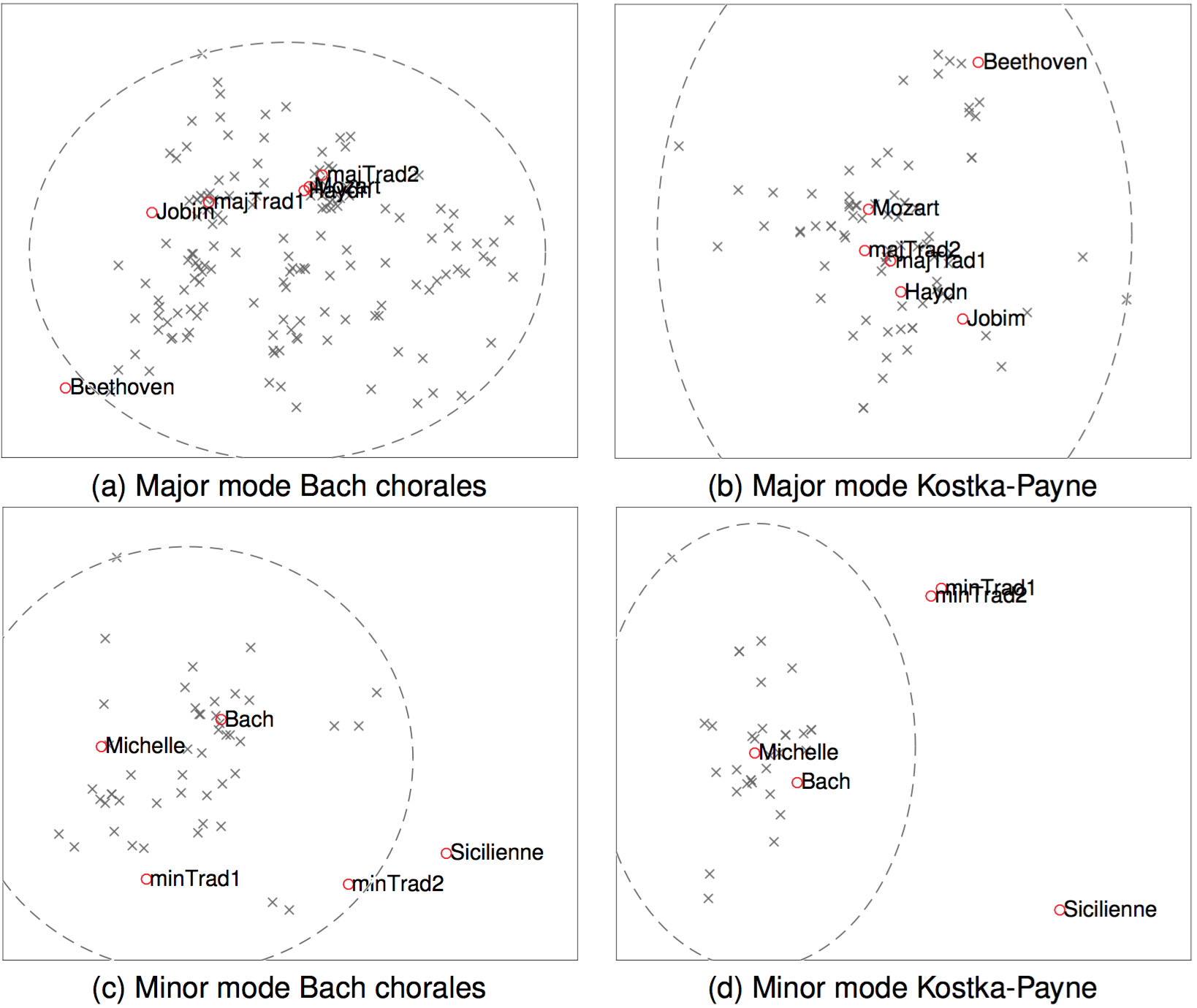
The original idiom harmonisation ($\mathcal{T_\mathcal{I}}$), as depicted in the examples in Fig. 11, are considered to form a cluster. To study the relative placement of the new harmonisations in every idiom’s cluster, the concept of cluster radius is used. Cluster radius is the maximum distance of all cluster members (harmonies in $\mathcal{T_\mathcal{I}}$) from the cluster centroid, which is the placed at the centre of mass of $\mathcal{T_\mathcal{I}}$. The radii of the clusters around their centroids are depicted by the dashed line ellipsoids in Fig. 11, while the ellipticity is due to different axis scales. A harmonic sequence that is outside an idiom’s radius, presents transitions in proportions that are not “usual” (in a statistical sense) within the training idiom. The novel system-generated harmonisations ($\mathcal{M_\mathcal{I}}$) that are outside an idiom’s cluster radius, are considered to constitute “uncommon” new harmonisations that explores new harmonic areas in an idiom.

The radius for each cluster and the distances of new harmonies from the cluster’s centroid are demonstrated in Tab. 7. One notices that for some corpora there is more than one melody that produces harmonisations outside the cluster’s radius, e.g., in Constantinidis major and Grieg, Kostka-Payne (Fig. 11 (d)), Hindemith and jazz minor. The Hindemith and jazz example harmonisations in Fig. 10 of the Sicilienne melody, which are outside the respective clusters’ radii, suggest that the general characteristics of the styles are locally preserved, even though the chord sequences as wholes are statistically “divergent” from the idiom. On the other hand, all the Kostka-Payne (Fig. 11 (c)) and jazz major new harmonisations are inside the cluster’s radius. The music-theoretic reasons for such differences, or the perceptual impact of harmonisations outside or inside an idiom’s radius are important subjects that should be addressed in future research.

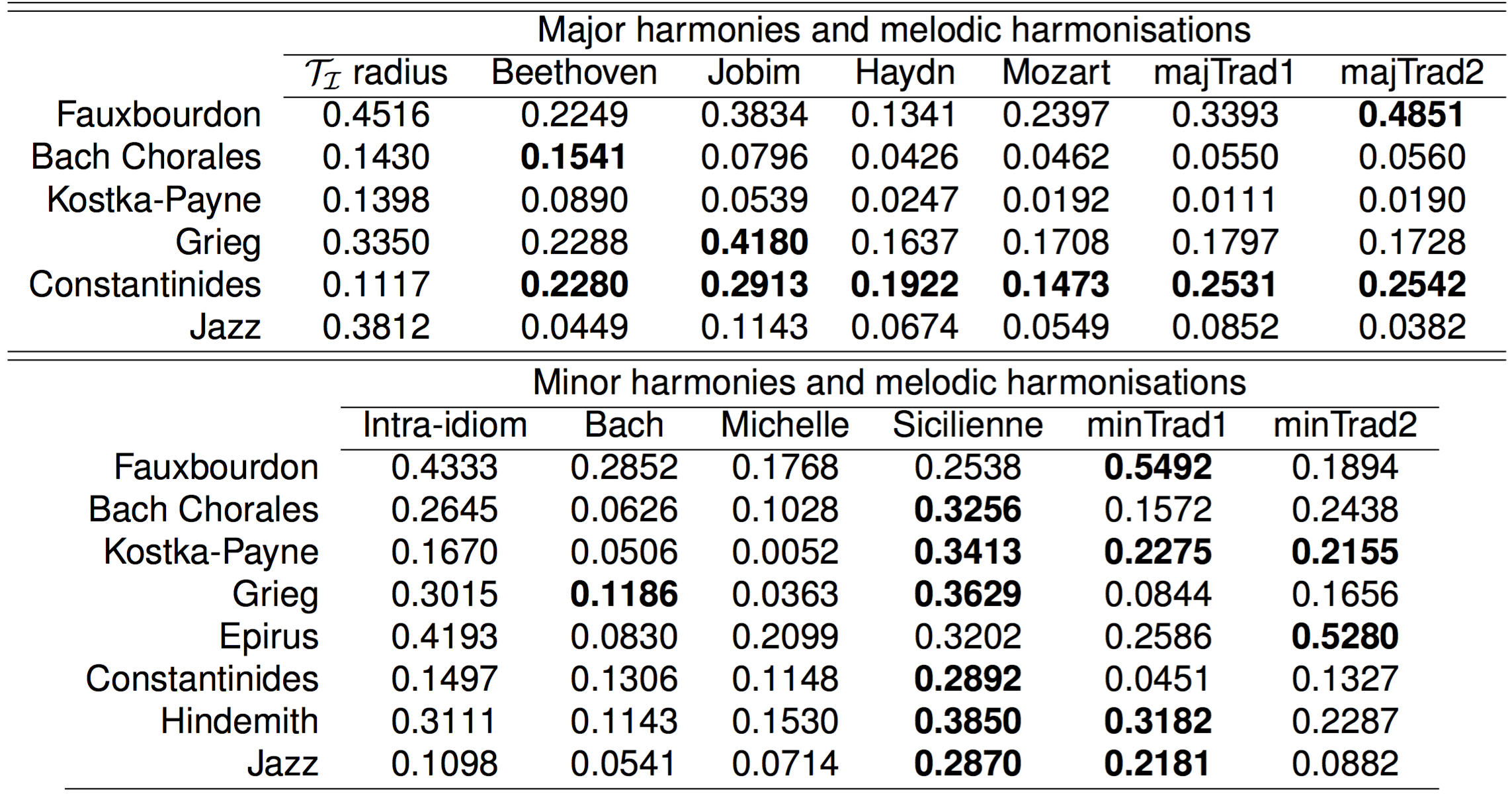
Depending on the melody, the system may either produce harmonisations that are similar to the original training harmonies, or be forced to produce harmonisations that are less similar. This fact is important in two respects: on one hand the system is able to mimic hierarchically structured processes through a Markov-based process (using induced constraints), while on the other hand new harmonic paths can be explored. For instance, harmonising the traditional or the Sicilienne melodies with a system trained with the Kostka-Payne corpus (Fig. 11 (d)), forces the system to “explore” new harmonic areas within the idiom and generate diverse novel harmonies, in contrast to the harmonisations of the Beatles and Bach melodies. The harmonies that excess an idiom’s radius, on the other hand, still reflect its learned characteristics, as indicated in the example of the Bach chorale harmonisation of the minor traditional melody 2 in Fig. 9 (c), even though it is placed remotely in Fig. 11 (c).

Interestingly, when the system is trained with the Bach chorales and the Kostka-Payne corpus, the relative positions of composed melodic harmonisations may be different. For instance, the harmonisations produced for the Mozart and Haydn melodies when trained with the Bach chorales (Fig. 11 (a)) are very similar (one is almost placed over the other), while training the system with the Kostka-Payne corpus harmonises these melodies quite differently (Fig. 11 (b)) – a fact that is possible due to the probabilistic mechanics behind the cHMM methodology. Furthermore, this is also a possible outcome in the proposed system, where even similar melodies can be harmonised in completely different ways if, for instance, different cadences are automatically selected, or, potentially, different intermediate chord constraints (or cadences) are selected by the user.

7 Concluding Remarks

Melodic harmonisation with automated means is a task that requires algorithms exhibiting both emergence of creativity and preservation of structure. The first approaches for automated melodic harmonisation included methodologies that were based on human-defined rules. The strength of these approaches is that the rules they incorporate preserve the hierarchical structure of harmony. Among their shortcomings, however, is the fact that different sets of rules describe different idioms and it is almost impossible for most idioms to formulate sets of rules that accurately describe their harmony. On the other hand, methodologies that utilise statistical learning can learn specific aspects of harmony from data, a fact that enables them to learn and create harmonies in different musical idioms. The main disadvantage of probabilistic methodologies is that they work in a rather “linear” chord-to-chord manner, disregarding higher-level structural relations between remote harmonic parts. The first contribution of the proposed melodic harmonisation system is the fact that it can learn from data of diverse music idioms, while at the same time preserve higher-level harmonic structure. Additionally, the system output is a complete harmonic realisation with chords being described not only as labels, but as note simultaneities. To this end, different harmonic learning modules are responsible for learning and composing different aspects of harmony, namely chord types, chord transitions, cadences, bass-voice movement, chord inversions and melody-to-bass note distances. Furthermore, the user can choose to import any desired chord at any location of the harmonisation, “derailing” the system from its trained harmonic course, thus forcing the system to take creative decisions and follow alternative harmonic paths.

The creative agility of the system is obvious when used to harmonise melodies with a variety of learned idioms. Therein, the implied harmony incorporated in the melody is blended with the learned harmony employed for the harmonisation, producing interesting harmonic output. By analysing several interesting examples with melodies being harmonised with harmonically “incompatible” learned idioms, it became obvious that the system invents new creative harmonic routes that to some extent constitute a blend of the incorporated harmonies. Therefore, the system exhibits adaptivity in learning and agility in expressing learned harmonic idioms in different and potentially alien harmonic environments, as imposed by a melody’s implied harmony. Another important aspect of the system is its ability to accommodate specific user preferences in harmony, expressed as chord constraints. The user is able to experiment by employing desired chords in any position of the melody, forcing the system to follow potentially radically different harmonic paths in order to satisfy the user-imposed constraints. The direct involvement of the user in the creativity loop, combined with the multiple potential harmonisations using different learned idioms, make the proposed system valuable not only as an autonomous creative tool, but also as a tool that enhances the creativity of the user.

The system is developed in the context of a wider research project, where conceptual blending (Fauconnier & Turner, 2003; Goguen, 2006) is studied as a generative means to creating new conceptual spaces (features and relations between them) by combining the elements of two input ones. Regarding the proposed system, learned probabilistic elements of different input idioms will be transformed in logic-related feature terms, while formal computational blending processes (Schorlemmer et al., 2014; Kaliakatsos-Papakostas et al., 2014a; Cambouropoulos et al., 2015) will create new elements and relations that creatively combine and extend the input idioms by generating new probabilistic relations between them. However, the system in its current form is still a valuable tool for potential user groups. For instance, composers are able to get a “batch” of creative ideas on harmonisation alternatives for a given melody within a few seconds. The system is able to provide very quickly several ideas on how a melody would be harmonised under different learned conditions, enhancing the composer’s creativity by providing many new ideas on the entire harmonisation or, at the very least, parts of it. Additionally, the composers are able to keep some parts of the harmonisation fixed (as chord constraints) and search for alternatives in focused areas. Furthermore, the system can be used for educational purposes, indicating to students which harmonisation follows the most “usual” harmonic paths for a given melody in diverse idioms. Students have the chance to explore creative ideas in a style-specific harmonic environment by imposing their desired chord constraints and studying the alternative harmonic routes that the system proposes in the context of a specific idiom.

References

1. Allan, M. & Williams, C.K.I. (2004). Harmonising chorales by probabilistic inference. Advances in neural information processing systems, 17, 25–32.